In de formule van het model wordt gebruik gemaakt van de aandelenkoers, de verwachte dividenden, de uitoefenprijs van de optie, verwachte rentetarieven, tijd tot expiratie en de verwachte volatiliteit.
In dit artikel bespreken we het Black-Scholes model, waarbij we kijken naar de aannames en de waarderingen op basis van de formule.
Bent u op zoek naar een broker om opties te handelen, klik dan hier.
Opties zijn complexe financiële instrumenten en brengen aanzienlijke risico’s met zich mee. Beleggers moeten zorgvuldig overwegen of ze geschikt zijn voor hun beleggingsdoelstellingen en risicobereidheid. Beleggers moeten ook hun kennis van de optiemarkt en verschillende strategieën vergroten voordat ze beginnen met handelen in opties.
Black-Scholes model
De term Black and Scholes verwijst naar drie concepten binnen de financiële wiskunde. We onderscheiden het Black-Scholes model, de Black-Scholes partiële differentiaalvergelijking en de daaruit afgeleide Black-Scholes formule. Deze concepten werden ontwikkeld in 1973 door de wetenschappers Fischer Black en Myron Scholes.
Het Black-Scholes model is een wiskundig model voor de financiële markt die derivaten bevat. Uit de parabolische partiële differentiaalvergelijking in het model, bekend als de Black-Scholes-vergelijking, kan men de Black-Scholes formule afleiden. Met deze formule kan een theoretische schatting worden gegeven van de prijs van Europese-stijl opties. Dit model toont bovendien aan dat de optie een unieke prijs heeft, gegeven het risico van het effect en het verwachte rendement ervan.
Het komt er in het kort op neer dat bovengenoemde personen een formule hebben ontwikkeld waarmee optieprijzen berekend kunnen worden. Later is het model nog verder ontwikkeld door Merton, waardoor men het soms ook heeft over het Black-Scholes-Merton (BSM) model. Myron Scholes ontving voor hun werk in 1997 de Nobelprijs voor de Economie, maar Black was toen echter al overleden.
Aannames black-scholes model
Het Black-Scholes-model gaat ervan uit dat de markt bestaat uit tenminste één risicovolle asset, meestal een aandeel. Daarnaast bestaat de markt ook uit één risicoloze asset, bijvoorbeeld cash of een staatsobligatie.
Vervolgens worden de volgende aannames gedaan voor de risicovolle asset:
- Het effect vertoont een stochastisch proces. Dat wil zeggen dat het effect moet voldoen aan de random-walk theorie. Specifieker: de geometric brownian motion (GBM).
- Het effect in kwestie keert geen dividenden uit.
- Het derivaat in kwestie is Europees, dat wil zeggen dat er slechts één moment is waarop een uitbetaling (afwikkeling) kan plaatsvinden.
Voor de ‘risicovrije’ asset (cash of staatsobligatie) nemen we het volgende aan:
- Er kan geld geleend en uitgeleend worden tegen een gelijke continue samengestelde rentevoet, welke constant blijft in de tijd.
- We kunnen voor elk bedrag aandelen kopen en verkopen zonder handelskosten.
- Mogelijkheid tot het lenen en uitlenen van elk bedrag, zelfs fractioneel, van contant geld tegen de risicoloze vergoeding.
- De markt kent geen arbitrage mogelijkheden.
Met bovenstaand model toonden Black en Scholes aan dat het voor Europese call en put opties mogelijk is om een afgedekte positie te creëren. Deze hedge bestaat uit een long positie in het aandeel en een short positie in de optie, waarvan de waarde niet zal afhangen van de prijs van het aandeel.
Hun dynamische afdekkingsstrategie leidde tot een partiële differentiaalvergelijking die de prijs van de optie bepaalde. De Black-Scholes formule is afgeleid uit deze vergelijking.
Hoewel het Black-Scholes model een belangrijke rol speelt in de theoretische waardering van opties, kent het model ook beperkingen. Zo gaat het onder meer uit van constante volatiliteit en een efficiënte markt. In de praktijk kunnen marktomstandigheden hiervan afwijken, waardoor de berekende prijzen kunnen verschillen van de werkelijke marktprijzen.
Waardering van opties met de Black-Scholes formule
De prijzen van opties worden bepaald met behulp van de Black-Scholes formule. De formule maakt gebruik van aandelenkoersen, strike prijzen van opties, tijd, volatiliteit en verwachte rentetarieven. De enige parameter die niet direct observeerbaar is op de markt, is de verwachte volatiliteit. Deze wordt vaak afgeleid uit de prijzen van reeds verhandelde opties (de zogenoemde ‘implied volatility’). Hieronder zullen we de formule kort toelichten.
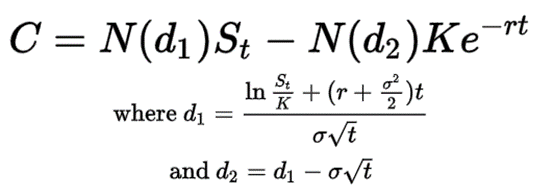
- C = call price (prijs van de call)
- N = cumulative distribution function of the normal distribution (cumulatieve verdelingsfunctie van de normale verdeling)
- St = spot price of the asset (huidige prijs)
- K = strike price (uitoefenprijs)
- r = risk-free interest rate (risicovrije rentevoet)
- t = time to expiration (tijd tot expiratie)
- σ = volatility of the asset (volatiliteit van de onderliggende waarde)
Wat betekent dit model voor optiebeleggers?
In moderne handelsomgevingen worden optieprijzen vrijwel realtime berekend, vaak met gebruik van het Black-Scholes model of aanpassingen daarvan. Dit draagt bij aan een transparanter prijsvormingsproces. Tegelijkertijd is het essentieel dat beleggers begrijpen dat de output van dit model slechts zo betrouwbaar is als de aannames waarop het gebaseerd is.
Het idee achter het model – het continu aanpassen van de afdekking van een positie (delta hedging) – vormt de basis voor veel hedgingstrategieën. Deze technieken worden echter voornamelijk toegepast door professionele partijen zoals banken en hedgefondsen, en vergen diepgaande kennis van risicomanagement en modellering.
Toegang tot de optiemarkt via LYNX
Voor beleggers die beschikken over voldoende kennis en ervaring met opties, biedt LYNX toegang tot een uitgebreid aanbod van Europese en Amerikaanse aandelen- en indexopties. Via het TWS handelsplatform of LYNX+ kunnen orders in opties en optiecombinaties efficiënt naar de beurs worden gestuurd.
Daarnaast zijn er tools beschikbaar die het analyseren en volgen van optietransacties ondersteunen. Deze tools zijn bedoeld om ervaren beleggers te helpen bij het structureren en beheren van hun strategieën.